PARADOJA DE SAN PETERSBURGO

En la teoría de probabilidad , la paradoja de San Petersburgo es una paradoja que consiste en un juego de apuestas con un valor esperado infinito. En esta situación, la teoría de decisiones recomienda que se admita cualquier apuesta por alta que sea, acción que ninguna persona con sentido común seguiría.

HISTORIA:

La formulación original de la paradoja aparece en una carta enviada por Nicolaus Bernoulli a Pierre de Montmort, el 9 de septiembre de 1713. Después de esto Nicolaus estuvo aún un tiempo intentando encontrar la solución al problema que él mismo se había planteado, pero finalmente en el año 1715 optó por consultar a su primo Daniel, al que reconocía una capacidad matemática superior a la suya. Por aquel entonces Daniel Bernoulli se encontraba en San Petersburgo, atraído junto con otros grandes científicos y pensadores de la época por las magníficas condiciones de estancia y trabajo ofrecidas por Pedro el Grande para hacer de esa ciudad el mayor foco de conocimiento de toda Europa. Tras su primera contestación, Daniel estuvo unos años reflexionando sobre el problema planteado, publicando su análisis y su propuesta de solución en 1738 en las Actas de la Academia de Ciencias de San Petersburgo, ciudad de donde proviene el nombre de la paradoja.

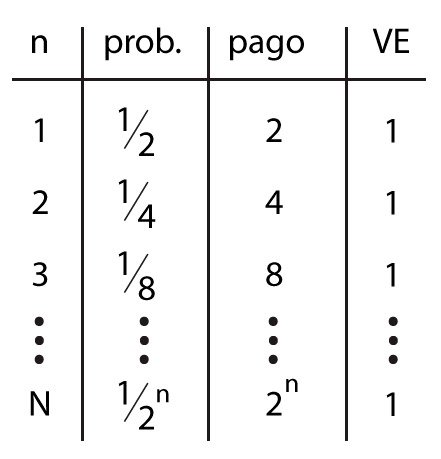
La formulación estándar de la paradoja de San Petersburgo es la siguiente: el jugador tiene que pagar una apuesta para participar en el juego. A continuación este realiza lanzamientos sucesivos de una moneda hasta que salga cruz por primera vez. Entonces se detiene el juego, se cuenta el número de lanzamientos que se han producido, y el jugador obtiene 2ⁿ monedas . Si sale cruz la primera vez el jugador gana ${\displaystyle 2^{1}=2}$ euros; si la cruz sale en el segundo lanzamiento gana ${\displaystyle 2^{2}=4}$ euros; si sale en el tercero ${\displaystyle 2^{3}=8}$; si en el cuarto ${\displaystyle 2^{4}=16}$,... ¿Cuánto estaría el lector dispuesto a pagar para jugar a este juego?